体积,而这个圆柱与粮囤的体积相等,即积一定,根据圆柱体积=πr2h可知,圆柱高h与半径的平方r2成反比例.由此列方程解.
【解法3】设圆柱粮囤高为h米.
麦堆底半径:25.12÷3.14÷2=4(米)
粮囤底半径:4÷2=2(米)
16=4h
h=4
答:这个圆柱形粮国的高是4米.
【评注】解法3的思路最简单、最灵活,运算最简便,是本题的最佳解法.
例119 一个圆锥体的体积是36立方分米,高是9分米,比与它等底的圆柱体的体积小12立方分米,这个圆柱体的高是多少分米?(天津市河西区)
【分析1】先求圆锥的底面积即圆柱的底面积,再求圆柱体积,最后求圆柱的高.
【解法1】圆柱底面积是多少?
36×3÷9=12(平方分米)
圆柱的体积是多少?
36+12=48(立方分米)
圆柱的高是多少?
48÷12=4(分米)
综合算式:(36+12)÷(36×3÷9)
=48÷12=4(分米).
【分析2】如果设圆柱高为h,那么它相当于高为3h的等底圆锥,而这的高与圆锥的体积成正比例.
【解法2】设圆柱体的高是h分米.
(36+12)∶3h=36∶9
答:这个圆柱体的高是4分米。
【评注】解法2的思路简单明白,运算最为简便,是本题的较好解法.本题还可用方程解,读者试解一下.
例120 如下图,求阴影部分的面积(单位:厘米).
(湖北省武汉市)
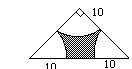
【分析1】从图中条件可知,三角形为等腰直角三角形,所以两个锐角都是45°.因此用三角形的面积分别减去三个扇形的面积,即得阴影面积.
【解法1】(10+10)×(10+10)÷2
=20×20÷2-3.14×25-3.14×25
=200-78.5-78.5=43(平方米)
【分析2】因为三个空白扇形恰好拼成180°的扇形,所以用三角形的面积减去圆心角是180°的扇形面积,即得阴影部分的面积.
【解法2】(10+10)×(10+10)÷2
=20×20÷2-3.14×10×10÷2
=200-157=43(平方厘米).
【分析3】同分析2.用三角形的面积减去半圆的面积,即得阴影部分的面积.
【解法3】(10×2)×(10×2)÷2-3.14×10×10÷2
=200-157=43(平方厘米).
答:阴影部分的面积是43平方厘米.
【评注】比较以上三种解法,解法3的思路较灵活,运算简便,是本题较好解法.
例121 右下图是由若干个1立方厘米的正方体木块摆成的图形,它的体积是多少立方厘米?
(广东省广州市越秀区)
上一页 [1] [2] [3] [4] [5] [6] 下一页
