例127 如图,求阴影部分的面积(单位:厘米).
(湖南省长沙市东区)
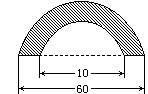
【分析1】先求大半圆的面积,再求小半圆的面积,用大半圆面积减去小半圆面积即得阴影部分的面积.
=1413-39.25
=1373.75(平方厘米).
【分析2】先求大圆面积,再求小圆面积,用大圆面积减去小圆面积,再除以2即得阴影部分的面积.
=(2826-78.5)÷2
=2747.5÷2=1373.75(平方厘米).
【分析3】本题是求半圆环面积.可先求圆环面积,再除以2即得.如果设大圆半径为R,小圆半径为r,那么圆环面积=πR2-πr2=π(R2-r2)
【解法3】R=60÷2=30(厘米)
r=10÷2=5(厘米)
3.14×(30×30-5×5)÷2
=3.14×(900-25)÷2
=2747.5÷2=1373.75(平方厘米).
【评注】比较以上五种解法,前四种解法的综合算式可通过乘法分配律相互转化,其中解法3的运算简便,是本题的较好解法.
例129 从一个长方体上截下一个棱长4厘米的正方体后,剩下的是一个长方体,它的体积是32立方厘米.原来长方体最长的一条棱是多少厘米?
(山西省太原市)
【分析1】因为截下的是正方体,所以剩下长方体的截面是正方形.因此可求出剩下长方体的长,再加上截下正方体的棱长,即得原来长方体的最长棱.
【解法1】剩下长方体的长?
32÷(4×4)=2(厘米)
原来长方体的最长棱?
2+4=6(厘米)
综合算式:32÷(4×4)+4
=32÷16+4=6(厘米).
【分析2】用剩下长方体的体积加上截下正方体的体积,即得原来长方体的体积.再根据“长方体体积=底面积×高”,用原长方体的体积除以底面积即得它的最长棱.
【解法2】截下正方体的体积?
4×4×4=64(立方厘米)
原来长方体的体积?
64+32=96(立方厘米)
原长方体的最长棱?
96÷(4×4)=6(厘米)
综合算式:(4×4×4+32)÷(4×4)
=(64+32)÷16=96÷16=6(厘米).
【分析3】根据“剩下的长方体体积加上截下的正方体体积等于原来长方体的体积”这一等量关系,列方程解.
【解法3】设原来最长棱x厘米.
32+4×4×4=(4×4)x
32+64=16x
x=96÷16
x=6
【分析4】用比例解法.因为长方体的体积÷高=底面积,底面积一定,所以长方体的体积和高成正比例.即长方体的体积与最长棱成正比例.
【解法4】设原来最长棱x厘米.
(4×4×4)∶4=(32+4×4×4)∶x
64∶4=96∶x
64x=4×96
x=6
答:原来长方体的最长棱是6厘米.
【评注】后三种解法都需要求出原来长方体的体积,再求原来的最长棱,运算较繁.解法1的思路简单明白,且运算简便,所以是本题的最佳解法.
例131 把一个高3分米圆柱体的底面分成许多个相等的扇形,然后把圆柱体切开,拼成一个与它等高的近似长方体,长方体的表面积比圆柱体的表面积增加12平方分米,原来圆柱体的体积是多少?
(福建省福州市)

上一页 [1] [2] [3] [4] [5] [6] 下一页
