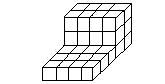
【分析1】把此图分为三层,最底层的长是5厘米,宽是4厘米,高是1厘米,由此可求底层的体积.同样可求第一层和第二层的体积,再将三层的体积加起来即得此形体体积.
【解法1】最底层的体积是多少?
5×4×1=20(立方厘米)
第一层和第二层的体积共多少?
4×2×2=16(立方厘米)
此形体的体积是多少?
20+16=36(立方厘米)
综合算式:5×4×1+4×2×2
=20+16=36(立方厘米).
【分析2】把这个形体切成一个长4厘米、宽3厘米、高1厘米和一个长4厘米、宽2厘米、高3厘米的两个长方体,求其体积和.
【解法2】4×3×1+4×2×3
=12+24=36(立方厘米).
【分析3】把原形体补充为一个长5厘米、宽4厘米、高3厘米的长方体,求出它的体积,再减去多补充的体积4×3×2=24(立方厘米),即得原形体的体积.
【解法3】5×4×3-4×3×2
=60-24=36(立方厘米).
【分析4】因为第一、二层共有4×2×2=16(块),第三层有4×5=20(块),三层共36块,并且每块1立方厘米,由此可求36块多少立方厘米.
【解法4】1×(4×2×2+4×5)
=1×(16+20)=36(立方厘米).
答:它的体积是36立方厘米.
【评注】以上四种解法各有特色,读者可根据自己的实际情况灵活选用.
例122 如图,已知圆的直径是8厘米,求阴影部分的周长和面积.
(陕西省西安市新城区)
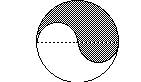
【分析1】图中阴影部分的周长是大圆半周长与小圆两个半周长的和,它的面积是大半圆的面积与小半圆面积的差,再加小半圆面积的和.
【解法1】
周长:3.14×8÷2+3.14×(8÷2)÷2×2
=25.12÷2+12.56÷2×2
=12.56+12.56=25.12(厘米)
=3.14×4×4÷2-3.14×2×2÷2+3.14×2×2÷2
=25.12(平方厘米).
【分析2】由图可知两个小半圆是相等的,因此阴影小半圆恰好补充空白小半圆,那么阴影面积等于大圆面积减去空白大半圆面积;阴影周长是小圆周长与大圆半周长的和.
=12.56+12.56=25.12(厘米)
=3.14×16-3.14×8
=3.14×(16-8)=25.12(平方厘米).
【分析3】因为大圆直径是小圆直径的2倍,所以小圆的周长和大圆的半周长相等,由此可知阴影部分周长恰是大圆的周长.将阴影小半圆移到空白小半圆使其重合,那么阴影部分恰是大半圆.
【解法3】周长:3.14×8=25.12(厘米)
=3.14×16÷2=25.12(平方厘米).
答:略.
【评注】比较以上三种解法,解法3的思路最直接最灵活,运算最简便,是最佳解法.
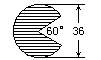
例123 如图,求阴影部分的面积(单位:厘米).
(辽宁省大连市中山区)
上一页 [1] [2] [3] [4] [5] [6] 下一页
