【分析1】先求出扇形的半径和圆心角的度数,再根据扇形面积公式求阴影的面积.
【解法1】半径:36÷2=18(厘米)圆心角:360°-60°=300°阴影面积:
=847.8(平方厘米).
【分析2】先求出扇形所在圆的面积,再求阴影部分占圆面积的几分之几,最后运用分数乘法应用题的解法求阴影面积.
=3.14×270=847.8(平方厘米).
【分析3】先求扇形所在圆的面积,再求空白扇形的面积,用圆面积减去空白扇形面积,即得阴影扇形的面积.
=3.14×18×18-3.14×18×3
=847.8(平方厘米).
【分析4】把扇形所在圆的面积看作“1”,那么空白扇形的面积占圆
的面积.
=3.14×270=847.8(平方厘米).
答:阴影部分的面积是847.8平方厘米.
【评注】比较以上四种解法,解法1的思路最简单,运算最简便,是本题最佳解法.
例124 在一个现代化的体育馆里铺设了30块长20米、宽3.5米、厚0.03米的硬塑地板,这个体育馆的面积有多少平方米?
(江苏省南京市鼓楼区)
【分析1】先求出每块硬塑板的占地面积,再求30块硬塑板的面积即体育馆占地面积.
【解法1】20×3.5×30
=70×30=2100(平方米).
【分析2】把这30块硬塑板平放成宽20米,长是30个3.5米的长方形,求出这个长方形的面积即体育馆的面积.
【解法2】3.5×30×20
=105×20=2100(平方米).
【分析3】把这30块硬塑板平放成长是30个20米、宽是3.5米的长方形,求出这个长方形的面积即体育馆的面积.
【解法3】20×30×3.5
=600×3.5=2100(平方米).
答:这个体育馆的面积有2100平方米.
【评注】解法1的思路最直接,解法最佳.
例125 求图中阴影部分的面积(单位:厘米).
(吉林省)
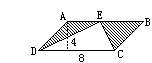
【分析1】先求平行四边形的面积,再求空白三角形的面积,用平行四边形的面积减去三角形的面积,即得阴影部分的面积.
【解法1】8×4-8×4÷2
=32-16=16(平方厘米).
【分析2】假设AE是6厘米,那么BE的长是8-6=2厘米.由此直接求出两个阴影三角形的面积,再求它们的面积和,即得阴影面积.
【解法2】假设AE长6厘米,那么BE的长是8-6=2厘米.
6×4÷2+2×4÷2
=12+4=16(平方厘米).
【分析3】因为三角形DEC和平行四边形等底等高,所以三角形DEC的面积是平行四边形面积的一半.由此求出平行四边形的面积再除以2即得阴影部分的面积.
【解法3】8×4÷2=16(平方厘米).
【分析4】把三角形ADE沿AB向右平移,使AD与BC重合,这样两个阴影三角形恰好拼成一个底是8厘米、高是4厘米的三角形,求出此三角形的面积即得阴影面积.
【解法4】8×4÷2=16(平方厘米).
答:阴影部分的面积是16平方厘米.
【评注】解法1和解法2虽然易于理解和掌握,但运算较繁.解法3和解法4的思路直接,简单灵活,运算简便,是本题最佳解法.
上一页 [1] [2] [3] [4] [5] [6] 下一页
